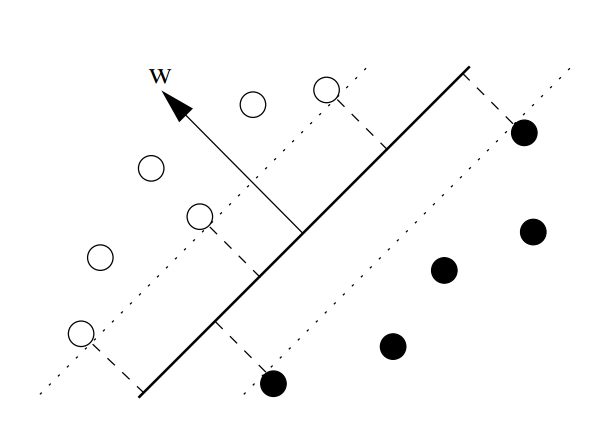
Support Vector Machine

Support Vector Machine is a binary parametric classifier that classifies items by creating a hyperplane between classes. This algorithm tries to find an optimum position for the hyperplane so that it splits the classes with the maximum margin between class items and minimum empirical risk. The items on the edges of the margin are called support vectors, as each item can be seen as a vector. An example of an SVM classifier’s hyperplane is shown in Figure below. It can be noticed that in a two-dimensional data set the hyperplane is represented as a line ¹.

One of the advantages of SVM is that it can use kernel trick. For a data set with nonlinear separation between classes, we can map the d-dimensional items x_i of input space into a high-dimensional feature space using a nonlinear transformation function ².

SVM has been used as an elementary stage to create rule-based classifiers. Nunez et al. ³ used rule extraction mechanism to extract rules from an SVM model generated via training samples. The rules are constructed using multiple of ellipsoid equations. While these rules might present a good visual illustration for the rules, especially for two-dimensional spaces, these equations have mathematical forms so that the generated rules are not intuitive and easy to understand as stand alone rules. Moreover, the ellipsoids are not one-to-one maps for the actual hyperplanes of SVM, so the rule-based classifiers are not as efficient as their SVM counterparts and they have a higher error rate.

Reference