Temporal Classification

Published on April 17, 2020 · 10 mins read

Temporal and sequence classification is an automatic system that assigns one of the predefined classes to the time series or sequence input. Many temporal classifications have been introduced that reuse traditional classification algorithms in terms of criteria and measurements crafted for temporal data. Three main methods exist for classifying temporal data set: distance-based, feature extraction-based and model-based 1.

Wang et al. 2 proposed a rule-based classification method for categorical and high-dimensional data sets that rely on calculating frequent item sets using frequent pattern mining and association rules, then using the highest confidence sets covering rules for grouping according to rule heads (class labels). This method has been found to result in an efficient and accurate rule-based classifier, but it might produce a very large number of rules, as they are extracted from association mining, which might be hard for humans to follow and comprehend. Moreover, to create the frequent item test, it is required to have training data sets, which might be expensive and labour intensive to acquire and deploy.

It is possible to use traditional classification algorithms (non-temporal) to classify temporal data set by using distance measures specially designed to evaluate distances in a temporal data set. Many temporal supervised and unsupervised algorithms use dynamic time warping (DTW) 3 to align between two sequences or time series and find the distance between them. This method was originally used in speech recognition to identify human speech patterns 4.

Difference between time alignment and Euclidean distance of two time series. Aligned points are indicated by arrows. From Keogh et al.
Difference between time alignment and Euclidean distance of two time series. Aligned points are indicated by arrows. From Keogh et al.

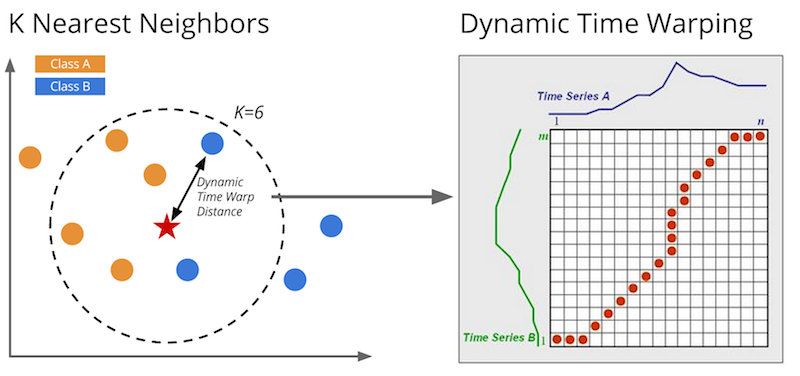
Dynamic time wrapping tries to find the best match between two time series to calculate the smallest distance between them, unlike Euclidean distance, which uses the one-to-one mapping between the same time points regardless of any time shift. Figure below compares these two distance measures. Dynamic time wrapping creates wrapping matrix which consists of Euclidean distances between every two points in both time series; then a local cost function finds the shortest path between two time series that represents the best match. Dynamic time wrapping has been implemented successfully in numerous temporal classification and clustering methods, but it has a drawback in using heuristic methods, which are inefficient due to searching for the best path in the wrapping matrix 5. The wrapping matrix and time wrapping distance between two time serris are shown in Figure below.

Calculating the distance between two time series using wrapping matrix. (a) Two similar but out of phase sequences. (b) Finding the optimal path (minimum distance) between the sequences which causes time wrap alignment between different time points of them. (c) The resulting alignment. From Keogh et al.
Calculating the distance between two time series using wrapping matrix. (a) Two similar but out of phase sequences. (b) Finding the optimal path (minimum distance) between the sequences which causes time wrap alignment between different time points of them. (c) The resulting alignment. From Keogh et al.

Distance-based K-Nearest Neighbours classification method (KNN) is used with temporal and sequential data with Euclidean distance measure 6. However, for complex time series, Euclidean distance is sensitive to the time fluctuation; thus DTW has been used 7. Figure below illustrates temporal KNN operation.

K-Nearest Neighbour using dynamic time wrapping for time series classification. From Regan
K-Nearest Neighbour using dynamic time wrapping for time series classification. From Regan

It is possible to use feature extraction in order to extract useful features from time series so that it becomes possible to use traditional classification methods to classify temporal data. Agrawal et al. 8 proposed the use of the Discrete Fourier Transform (DFT) to transform a sequence from the time domain to the frequency domain. Using DFT allows selection of the most important frequencies then representing them back in the original dimensional space. The DFT has an important property as it can ignore shifts and find similar sequences because the Fourier coefficient is invariant for shifts.

Chan et al. 9 used DWT to translate each time series from the time domain into the time/frequency domain. This transformation is linear as it changes the original time series into various frequency components in a lossless transformation. The sequence is then represented by its features, expressed as wavelet coefficients. Only a selected number of coefficients are necessary to represent the original time series, which allows a better and efficient use of the available classification algorithms.

Douzal-Chouakria et al. 10 used classification trees to classify time series data by introducing new splits for the tree nodes using time series proximities, relying on adaptive metrics considering behaviours and values. Other methods use SVM as a temporal data classifier using different kernels 11.

Model-based classifiers can also be used for temporal and sequential classifications, like Naive Bayes sequence classifier 12 and Hidden Markov Model 13. In the training step, the parameters of the model are created and trained depending on some assumptions, and a set of parameters describing probability distributions. In the classification step, a new sequence is assigned to the class with the best possible similarity 14.

References

  1. Laxman, S. and Sastry, P. P. (2006) ‘A survey of temporal data mining’, Sadhana, 31(April), pp. 173–198. doi: 10.1007/BF02719780. ↩

  2. Wang, J. and Karypis, G. (2005) ‘HARMONY: Efficiently Mining the Best Rules for Classification’, Proceedings of the 2005 SIAM International Conference on Data Mining, pp. 205–216. ↩

  3. Berndt, D. and Clifford, J. (1994) ‘Using dynamic time warping to find patterns in time series’, AAAI-94 Workshop on Knowledge Knowledge Discovery in Databases, 10(16), pp. 359–370. ↩

  4. Rabiner, L. and Juang, B.-H. (1993) Fundamentals of speech recognition. PTR Prentice Hall. ↩

  5. Keogh, E. and Ratanamahatana, C. A. (2005) ‘Exact indexing of dynamic time warping’, Knowledge and Information Systems, 7, pp. 358–386. doi: 10.1007/s10115-004-0154-9. ↩

  6. Wei, L. and Keogh, E. (2006) ‘Semi-supervised time series classification’, Proceedings of the 12th ACM SIGKDD international conference on Knowledge discovery and data mining - KDD ’06, p. 748. doi: 10.1145/1150402.1150498. ↩

  7. Kaj’an, L. et al. (2006) ‘Application of a simple likelihood ratio approximant to protein sequence classification’, Bioinformatics, 22(23), pp. 2865–2869. doi: 10.1093/bioinformatics/btl512. ↩

  8. Agrawal, R., Faloutsos, C. and Swami, A. (1993) ‘Effcient Similarity Search In Sequence Databases’, Foundations of data organization and algorithms. Springer, pp. 69–84. ↩

  9. Chan, K. and Fu, A. W. (1999) ‘Efficient Time Series Matching by Wavelets’, Data Engineering, 1999. Proceedings., 15th International Conference. IEEE, pp. 126–133. ↩

  10. Douzal-Chouakria, A. and Amblard, C. (2012) ‘Classification trees for time series’, Pattern Recognition, 45, pp. 1076–1091. doi: 10.1016/j.patcog.2011.08.018. ↩

  11. Sitaram, R. et al. (2007) ‘Temporal classification of multichannel near-infrared spectroscopy signals of motor imagery for developing a brain-computer interface’, NeuroImage, 34(4), pp. 1416–1427. doi: 10.1016/j.neuroimage.2006.11.005. ↩

  12. Tseng, V. S. and Lee, C. H. (2009) ‘Effective temporal data classification by integrating sequential pattern mining and probabilistic induction’, Expert Systems with Applications, 36(5), pp. 9524–9532. doi: 10.1016/j.eswa.2008.10.077. ↩

  13. Oates, T., Firoiu, L. and Cohen, P. (1999) ‘Clustering time series with hidden Markov models and dynamic time warping’, Proceedings of the IJCAI-99 workshop on neural, symbolic and reinforcement learning methods for sequence learning, pp. 17–21. ↩

  14. Xing, Z., Pei, J. and Keogh, E. (2010) ‘A brief survey on sequence classification’, ACM SIGKDD Explorations Newsletter, 12(1), p. 40. doi: 10.1145/1882471.1882478. ↩


Polla Fattah
«Previous Posts Next»