Internal criteria measure the ‘goodness’ of clusters for the data by extracting information from data and clusters alone, such as the compactness of data points inside one cluster and the separation of clusters from each other ¹. These criteria were used as part of the cost function, to determine the quality of the selected classification rules in each time point, and to compare different clustering algorithms’ performances, as presented in chapter six.

Dunn Index

This index calculates the ratio of minimum distance between clusters to the maximum distance between any two instances of the same cluster ²:

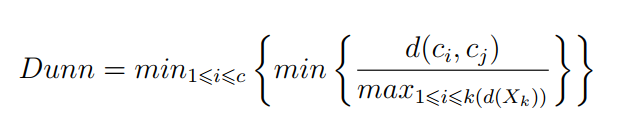
Where c_i, c_j ∈ c of size m and the maximum distance can be computed from the mean or between all pairs. A larger value for Dunn index means, better clustering output, because it means that the closest instances between two clusters are larger than the distance between two farthest instances in the same cluster ³.

Davies-Bouldin Index

This measure is introduced by Davies et al. ⁴. It calculates internal cluster compactness and inter cluster separation by producing the ratio of spreading sample points around mean (i.e. variation) to the distance between mean of clusters ¹.

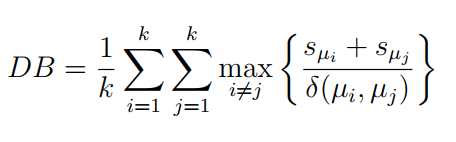
Where k is number of clusters, s_μi and s_μj are the spread of points around any two clusters cluster mean “Centroid”, and δ(μ_i, μ_i) denotes the mean of both clusters.

A smaller value of this measure indicates better the clustering, as in such cases the clusters are well separated and each cluster is well represented by its mean; in other words, larger values mean better compacted instances in the clusters and clusters that are well separated from each other ³.

SD

This measure is introduced by Halkidi et al. ⁵. It calculates the average scattering for clustering and total separation among clusters.

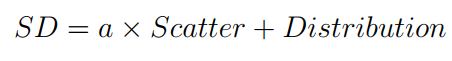
Where a is a weighting factor equal to the maximum distance of two instances in the data set. The Scatter indicates the average compactness of clusters. A smaller value of Scatter is a signal for a compact cluster, and its the value increases for less compact clusters. The Distribution is the measure of the total separation between clusters. A larger value Scatter indicates better clustering and a smaller value of this term indicates greater proximity between clusters to each other. Scatter, and Distribution have different ranges so that a (the weighting factor) is important to maintain the balance between them. As SD measure is a total of Scatterer and Distribution so that the smaller SD value indicates better clustering ⁵.

sdwb

This measure is introduced by Halkidi et al. ⁶. The S_Dbw index is similar to SD index as it measures the intracluster and intercluster variances ¹. The definition of S_Dbw indicates that both criteria of “good” clustering (i.e. compactness and separation) are properly combined, enabling reliable evaluation of clustering results.

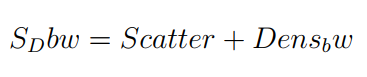
As with SD, the Scatter indicates the average compactness of clusters, smaller Scatter value indicating a compact cluster, with an increased value for less compact clusters. Dens_bw(c) indicates the inter-cluster density by calculating the average number of points between the clusters in relation with density within clusters. Thus a small value of Dens_bw means good separation among clusters. As in SD, a smaller value of this measure is an indication of well defined clustering ⁶.

---

Reference

Polla Fattah

---